原帖由 桺漫3 于 2008-7-18 10:40 发表
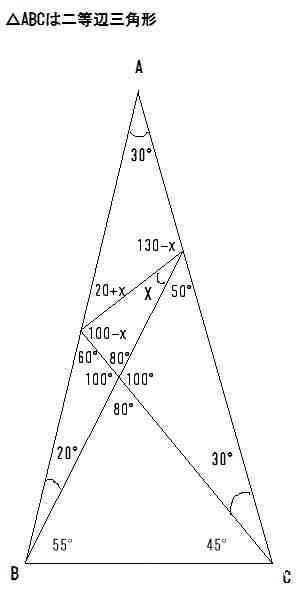
當然不是小學題目,還要考慮邊長比例和角度關係。
假設底邊長2,腰就長1/cos75°
答案是arctan(((2/3)^0.5*sin20°)/(sin75°/sin45°-(2/3)^0.5*cos20°))


原帖由 桺漫3 于 2008-7-18 10:40 发表
當然不是小學題目,還要考慮邊長比例和角度關係。
假設底邊長2,腰就長1/cos75°
答案是arctan(((2/3)^0.5*sin20°)/(sin75°/sin45°-(2/3)^0.5*cos20°))
原帖由 可以 于 2008-7-18 14:49 发表
我给的题 答案是30度没错,不过你没用初等几何的方法证明
楼主给的题 答案不是30度,只是接近30度。而且不能用初等几何的方法得到结果,想得到精确解需要解析几何的方法
原帖由 可以 于 2008-7-18 14:49 发表
我给的题 答案是30度没错,不过你没用初等几何的方法证明
楼主给的题 答案不是30度,只是接近30度。而且不能用初等几何的方法得到结果,想得到精确解需要解析几何的方法




原帖由 可以 于 2008-7-18 15:44 发表
:noway: 三角函数是高中内容,你小学就是上奥校也不可能学到。
楼主给的题只能硬算。添加辅助线或许可以简化计算
我给的题是可以用初中几何得到答案的。而且答案不是28-9度,而是精确的30度
附 初中几何教 ...
原帖由 可以 于 2008-7-18 17:19 发表
我还是不能相信你小学这么imba:noway:
按照 小学数学教学大纲 最多也就学学平行线,内角和180度。连同位角 对角线都没有,更不要说正弦/余弦定理本身的证明步骤了。
http://math.cersp.com/CourseStandard/CEDU ...


原帖由 可以 于 2008-7-18 17:19 发表
我还是不能相信你小学这么imba:noway:
按照 小学数学教学大纲 最多也就学学平行线,内角和180度。连同位角 对角线都没有,更不要说正弦/余弦定理本身的证明步骤了。
http://math.cersp.com/CourseStandard/CEDU ...



原帖由 hettyw 于 2008-7-18 17:04 发表
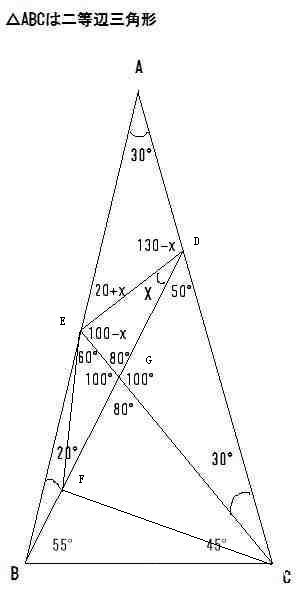
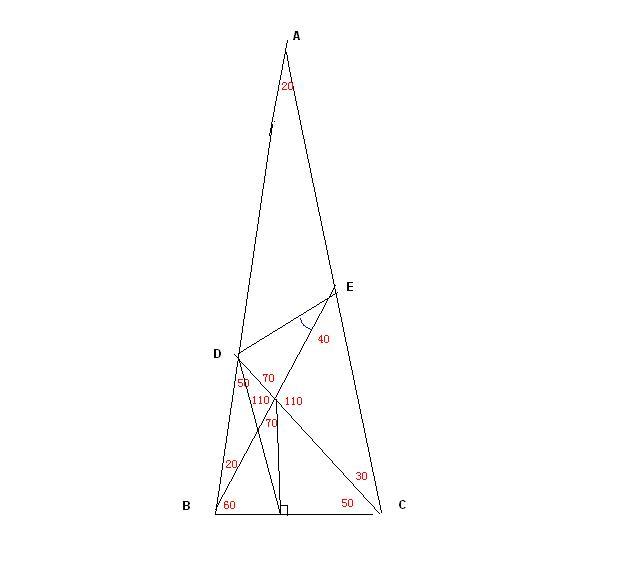
添加辅助线EF,使角BEF=10度,连接FC。
310533
做法如下:
310532
刚才用word打出来,才发现刚才后来算的时候带错数字了,所以答案有一点偏差,现在的答案是29°29'45"。
原帖由 驴子 于 2008-7-18 18:54 发表
你既然用正弦公式,那为什么不能直接在现成的三角形BCE,BCD和CDE里面用,非要去添加辅助线呢?
三角形BCE和BCD的所有角都是已知的,可以分别求出CE和CD相对BC的比值,CD和CE又在三角形CDE里面分别对应两个和x相关 ...





| 欢迎光临 人在德国 社区 (http://rs238848.rs.hosteurope.de/bbs/) | Powered by Discuz! 7.2 |